
[출처] : https://programmers.co.kr/
문제
Leo는 카펫을 사러 갔다가 아래 그림과 같이 중앙에는 노란색으로 칠해져 있고 테두리 1줄은 갈색으로 칠해져 있는 격자 모양 카펫을 봤습니다.

Leo는 집으로 돌아와서 아까 본 카펫의 노란색과 갈색으로 색칠된 격자의 개수는 기억했지만, 전체 카펫의 크기는 기억하지 못했습니다.
Leo가 본 카펫에서 갈색 격자의 수 brown, 노란색 격자의 수 yellow가 매개변수로 주어질 때 카펫의 가로, 세로 크기를 순서대로 배열에 담아 return 하도록 solution 함수를 작성해주세요.
제한사항
- 갈색 격자의 수 brown은 8 이상 5,000 이하인 자연수입니다.
- 노란색 격자의 수 yellow는 1 이상 2,000,000 이하인 자연수입니다.
- 카펫의 가로 길이는 세로 길이와 같거나, 세로 길이보다 깁니다.
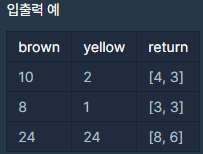
입출력 예 설명
접근
우선 그림과 같이 나오려면 최소한 가로와 세로가 3이상은 되어야 한다.
따라서 반복문을 3부터 시작하게 하였고 전체크기/3 까지 반복하게 하여서 가로와 세로를 구하도록 하였다.
갈색과 노란색을 더하면 전체 크기가 되기 때문에 이를 반복문을 돌려가면서 나눈나머지가 0이라면
i와 all/i 는 가로와 세로의 후보가 된다.
그리고 노란색의 넓이는 가로-2 * 세로-2 이므로 이 조건을 만족하는 i를 구하면 가로와 세로의 길이가 나오는데 문제에서 가로길이가 세로보다 길거나 같다 했기 때문에 sorted의 reverse를 이용해서 배열에 넣어준다.
def solution(brown, yellow):
all=brown+yellow
for i in range(3,(all//3)+1):
if all%i == 0:
if all//i >=i:
a = all//i
if yellow == (i-2)*(a-2):
return sorted([i,a],reverse=True)결과
다른사람의 풀이
약수를 이용한 풀이이다.
여기에서는 노란색(개편전에는 빨간색이라 풀이에서 red로 되어있다.)의 넓이를 이용해서 풀었다.
노란색의 가로 세로를 각각 a,b라고 가정하고 노란색이 나눴을때 0이되는 a를 구하면 자동으로 b가 구해지고 이는 약수의 성질인 '임의의 자연수 N의 약수들 중에서 두 약수의 곱이 N이 되는 약수 A와 약수 B는 반드시 존재한다' 이를 이용하면 아래의 코드처럼 반복문이 노란색의 1/2제곱만큼만 돌면된다.
def solution(brown, red):
for i in range(1, int(red**(1/2))+1):
if red % i == 0:
if 2*(i + red//i) == brown-4:
return [red//i+2, i+2]또다른 풀이로는 갈색과 노란색에 대한 식을 세우면 2차방정식이 되는데 이를 근의공식에 대입해서 푼 풀이도 있다.
import math
def solution(brown, yellow):
w = ((brown+4)/2 + math.sqrt(((brown+4)/2)**2-4*(brown+yellow)))/2
h = ((brown+4)/2 - math.sqrt(((brown+4)/2)**2-4*(brown+yellow)))/2
return [w,h]'알고리즘' 카테고리의 다른 글
| [프로그래머스 - Level 2] H-Index (0) | 2021.11.10 |
|---|---|
| [프로그래머스 - Level 2] 구명보트 (0) | 2021.11.08 |
| [프로그래머스 - Level 2] 올바른 괄호 (0) | 2021.11.03 |
| [프로그래머스 - Level 2] 땅따먹기 (0) | 2021.10.29 |
| [프로그래머스 - Level 2] N개의 최소공배수 (0) | 2021.10.26 |
